上帝會允許孩子們得癌症嗎?可能是...
我一直在試圖理解Karma-kun在考試總決賽中的數學問題。
我搜索了參考文獻,並對該問題進行了解釋,但無濟於事。我仍然無法理解對該問題的可怕解釋,而答案是假設您知道他們的思考過程,而我不是。
這是問題的英文翻譯:
young-il-long-kiyoshi.tumblr.com/post/125623681248/關於最後的數學問題的主題
我發現另一個鏈接提到了問題但沒有解釋。
Angryanimebitches.com/2016/03/assassination-classroom-season-2-episode-12-theprincipal-is-a-sore-loser/
他們也是youtube視頻,解釋了Karma-kun的答案,但即使是他的解釋,我仍然無法理解他如何得出這樣的結論:中心原子的面積等於立方體的面積除以二的一半。 a ^ 3/2
影片連結: 怪異的幾何(暗殺教室S2 E12)
我發布此消息的原因是,如果沒有線程詢問,我沒有其他方法可以理解問題。
我只想從“高中”的角度來解釋答案,而不是專業的博士學位級別...
我不想听到“等距”,“無窮小”,“頂點”或我無法理解的任何其他技術術語。
我知道我需求太多,但請幫助我了解Karma-kun是如何得到的 a ^ 3/2。我從業力中獲得的唯一觀點是,所有8個原子形成了它們自己的立方體,並且該虛構立方體的中點等於8個單獨立方體中的所有原子。
影片也這麼說,但是世界上的 1/8 到 2A?接著 a ^ 3/2
如下所示:
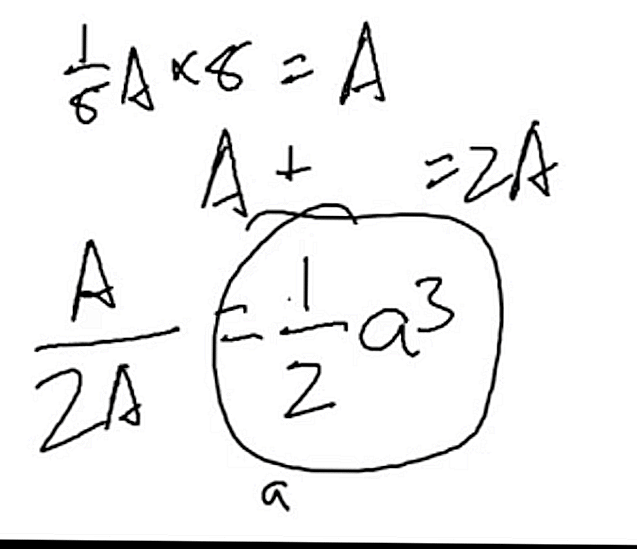
- 對於淺野坤的求解方法,我認為? math.stackexchange.com/questions/3193480 / ...
晶格中的所有原子都是相同的。假設頂點上一個原子的體積(不是角,如果是角,則需要稍微不同的推理)為B。頂點上的每個原子佔據立方體的(1/8)B。參見圖。
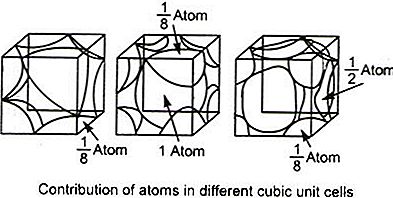
對於長度為a的立方體,它由體積為D的中心原子A和頂點處的8個原子組成,每個原子佔據立方體的(1/8)B。因此,
一種3 = D + 8×(1/8)B
但是,由於我們知道頂點上的原子實際上與中心原子相同,所以體積B等於D,因此,
一種3 = B + 8×(1/8)B ==> B =(1/2)a3
優質教育
您提到的所有技術術語都是我在高中時學到的。正如業力所說,這個問題並不難。這是數學和化學的綜合問題。
7- 1但我認為您應該在數學論壇而不是在這裡提問。看起來很尷尬。
- 但是為什麼呢 超過2 在公式a ^ 3/2中
- 此處的2以上只是告訴您,對於一個立方體,只有一半的體積是特定原子A佔據的體積,其餘的體積將由其他原子共享。
- 所以,如果我正確地跟隨你, A / 8 * 8 = A,並且八個頂點佔據2個原子,這意味著 2A。然後因為 一種 是立方體的一半,那麼我們 A / 2A...併計算原子的體積,我們將 x,y,z 這是 3D 然後我們得到公式來查找立方體的面積 a ^ 3 正確的?那麼我們一半 超過2? a ^ 3/2
- 不,頂點處的八個原子佔據了立方體中一個原子的空間。 A / 2A用於查找中心原子所佔體積與包含中心原子和頂點處原子的總體積之比。因此,據此我們知道原子A佔據了立方體體積的1/2,因而佔據了a ^ 3/2。
我知道我遲到了這個問題,但這是一個更簡單的解釋。我只是在動漫中遇到了這個問題,想在他們給出答案之前解決它。
好的。您有一個中間有一個原子的立方體。您要做的是將多維數據集分成八塊。拿其中一件。在對角(頂點)上有兩個原子。這些原子之一是中心原子[A] 0,另一個原子是邊緣原子。按照簡單的邏輯,立方體的八分之一正好比另一個原子更接近一個原子。其他所有8個零件都是這樣,因此更靠近中心原子的立方體的體積僅為總體積的一半。
這個問題比它看起來要簡單得多,在我意識到自己很笨之前,我承認用幾何圖形計算體積。它不需要太多的數學運算。只是紮實的邏輯和一點點機靈。
據推測,漫畫中的答案本身甚至是不正確的。如果原子在每個立方體中佔據相同的空間量,則它們將是(a)(不可見線)的一半。實際上,您可以將其插入用於求解球體體積的公式,該球體體積是3乘以pi乘以r的3倍。在這種情況下,您的r(半徑)為a / 2(因為原子佔據相同的原子)空間,因此一個原子將佔據不可見線的一半)
基本上,你會做V = 4/3 *π*(a / 2)^ 3
V = 4/3 *π* a ^ 3/8
V = 4(在4/3中)抵消了8(在a ^ 3/8中),因此得到1/3 *π* a ^ 3/2
V =π* a ^ 3/6
雜項:* =次,^ =冪,π= pi。